

Rounded off to three significant figures, the answer would be 1.90 x 10 3 years. We look it up and find it to be 5730 year. The problem does not provide the half-life of C-14. N = 0.330973 <- the number of half-lives elapsed Solution: (1/2) n = 0.795 <- n is the half-life, 0.795 is the decimal amount of C-14 remaining

N = 1.20956 <- the number of half-livesĠ.00930 yr times (365 day / yr) times (24 hr / day) = 81.468 hrīonus Example: A scrap of paper taken from a Dead Sea scroll was found to have a C-14/C-12 ratio of 0.795 times than found in plants living today. (1/2) 4 = 0.0625 <- decimal amount remaining after four half-livesĮxample #9: Find the half-life of an element which decays at a rate of 3.402% per day.Ĭomment: you could set up a spreadsheet and do it by brute force, subtracting 3.402% of the material on hand each day, with the half-life being the number of days needed to arrive at 50%.Įxample #10: The half-life of In-111 is 0.007685 years how long (in hours) would it take for the amount of In-11 to decrease to 43.24% of its initial amount?

Solution: 30 s / 7.5 s = 4 <- four half-lives elapsed during the 30 s If you currently have 73.3 g of P-32, how much P-32 was present 4 days ago?ġ) How many half-lives have elapsed in 4 days?Ģ) The decimal amount that remains after 0.27972 half-lives have elapsed:Įxample #8: If a sample contains 144 atoms of Au-179 (half-life = 7.5 s), approximately how many such atoms were present 30 seconds earlier? Sometimes, you will see the equation expressed thusly:Įxample #7: P-32 is radioactive isotope with a half-life of 14.3 days. It's the amount that remains that goes into the calculation. Many times, a problem will specify how much has decayed and you must use that information to determine how much remains. I would like to stress that the decimal amount is the amount that remains after a given number of half-lives. Just below are the amounts remaining after 2, 3, and 4 half-lives. However, please be aware that it is the decimal amount that will be used in the various calculations, not the percentage. At this point 0.5 of the original amount remains. This second example shows one half-life elapsed. Keep in mind that the decimal amount times 100 becomes the percentage. In other words, at the very start, before any decay has taken place, 100% of the material is on hand. The 1 represents the decimal fraction remaining. In this example, zero half-lives have elapsed. Let us use several different half-lives to illustrate this equation. (1/2) number of half-lives = decimal amount remaining
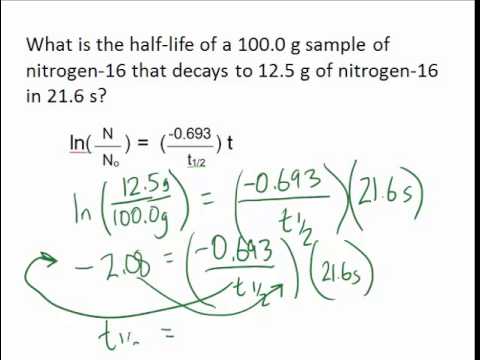
The order in which you use them depends on the data given and what is being asked. And that will be a good thing.ĭoing half-life problems is focused on using several equations. Later on, you may learn that approach to half-life calculations, one that uses calculus to develop the concept. What follows does not explicitly use the general chemical concept of kinetics. ChemTeam: Half-Life Radioactivity: Half-Life Ten Examples Probs 26-40 Probs 1-10 Problems involving carbon-14 Probs 11-25 Examples and Problems only (no solutions) Return to Radioactivity menu


 0 kommentar(er)
0 kommentar(er)
